Как применить теорию матриц в повседневной жизни и профессиональной деятельности

Когда мы слышим о теории матриц‚ в большинстве случаев перед глазами возникает сложная математическая концепция‚ используемая в научных исследованиях‚ инженерии или программировании. Но мало кто задумывается о том‚ как эта теория может быть применена в нашей повседневной жизни. Сегодня мы расскажем о том‚ как использовать матричные подходы для решения реальных задач‚ улучшения анализа информации и повышения эффективности в разных сферах.

На самом деле‚ матрицы — это удобный инструмент для моделирования и анализа множества процессов и ситуаций. Они позволяют систематизировать данные‚ находить взаимосвязи и оптимизировать решения. Давайте вместе разберемся‚ как теорию матриц можно внедрить в практические области‚ будь то личное развитие‚ бизнес‚ анализ данных или обучение новому.

Что такое матрица и зачем она нужна?

Определение и основные свойства

Матрица — это прямоугольная таблица чисел‚ символов или функций‚ упорядоченных по строкам и столбцам. В математике она служит инструментом для представления и обработки больших объемов данных‚ а также для выполнения разнообразных вычислительных операций. Каждая ячейка матрицы содержит элемент‚ который можно интерпретировать по-разному: как значение‚ коэффициент или параметр.

Основные свойства матриц:

Размерность: количество строк и столбцов‚ например‚ 3×3 или 2×5;
Определитель: число‚ которое показывает‚ есть ли у матрицы обратная;
Транспонирование: отражение матрицы относительно главной диагонали;
Умножение и сложение: операции‚ позволяющие сочетать матрицы для получения новых данных.

Примеры использования матриц

Область применения	Описание
Финансовый анализ	Моделирование инвестиционных портфелей‚ расчет рисков‚ оптимизация активов.
Логистика и маршрутизация	Рационализация маршрутов‚ расчет времени и затрат на перемещение грузов.
Обработка изображений	Фильтрация‚ сжатие и распознавание изображений с помощью матричных преобразований.
Обучение и развитие	Создание алгоритмов оценки навыков или поведения на основе данных.

Практические способы применения теории матриц в жизни

Анализ и систематизация информации

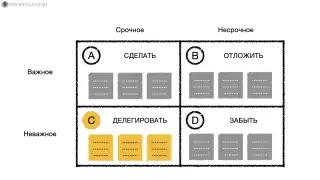
Одним из наиболее распространенных применений матриц является структурированный анализ данных. Когда у нас есть множество параметров: факты‚ оценки или показатели‚ — удобно представить их в виде таблицы. Это позволяет увидеть взаимосвязи‚ выявить тенденции и сделать выводы.

Например‚ при анализе качества работы сотрудников можно создать матрицу‚ в которой строки — это сотрудники‚ а столбцы, показатели эффективности:

Качество выполнения задач
Соблюдение сроков
Клиентский отзыв

Такая матрица помогает определить лидеров и слабых звеньев‚ организовать работу более эффективно.

Оптимизация маршрутов и задач

В бизнесе и личной жизни мы постоянно сталкиваемся с необходимостью планировать маршруты или последовательность действий. Матричные методы позволяют решить задачу наилучшей оптимизации.

К примеру‚ при планировании поездки‚ чтобы посетить все точки с минимальными затратами времени и ресурсов‚ можно составить матрицу расстояний или времени между местами. Затем применить алгоритм поиска минимального пути — например‚ алгоритм «Коммивояжера».

Это существенно сокращает затраты и дает эффективное решение даже в условиях множества вариантов.

Обучение и развитие навыков с помощью матриц

Если вы хотите понять‚ как развивать конкретные навыки или знания‚ можно составить матрицу‚ где строки — ваши умения‚ а столбцы — критерии оценки или параметры развития:

Текущий уровень
Желаемый уровень
Ресурсы для повышения
Дедлайны

Такая схема помогает систематизировать план развития и отслеживать прогресс.

Как научиться работать с матрицами: практические советы

Понимайте основную логику: транспонирование‚ умножение‚ обратные матрицы. Это базовые операции.
Практикуйтесь на простых задачах: создавайте таблицы‚ решайте задачи на умножение матриц.
Используйте специальное программное обеспечение: Excel‚ Google Sheets‚ MATLAB или Python.
Разрабатывайте свои проекты‚ где будете использовать матричные модели: например‚ планирование бюджета или анализ навыков.
Обучайтесь постоянно: смотрите видеоуроки‚ читайте статьи и книги по теории матриц и ее применению.

Понимание сути и практики позволит вам не только понять теорию‚ но и внедрить ее в повседневные задачи.

Ответ на популярный вопрос

Вопрос: Могу ли я применить теорию матриц‚ если у меня нет глубоких знаний в математике?

Конечно! Многие аспекты работы с матрицами не требуют профессиональных математических навыков. Сегодня доступны простые инструменты‚ такие как таблицы Excel‚ которые позволяют легко создавать и вычислять матричные данные. Главное — понять концепцию и методы применения‚ а сложная математика нужна только в более глубоких или специфических случаях. Для начинающих важно освоить основные операции и научиться интерпретировать полученные результаты — это уже поможет значительно упростить решение задач в повседневной жизни и бизнесе.

Подробнее о применениях теории матриц: полезные ссылки и материалы

Подробнее

Матричные операции в Excel	Обучающие курсы по теории матриц	Практические кейсы использования матриц	Матричные алгоритмы в программировании	Обработка данных с помощью матриц
Примеры анализа в бизнесе	Математические основы для новичков	Матричные преобразования в визуализации	Расчет оптимальных маршрутов	Обучающие материалы по программированию матриц