- Как применить теорию матриц в реальной жизни: практические советы и примеры
- Что такое матрица и как она представлена?
- Применение теории матриц в различных сферах жизни
- Обработка изображений и компьютерное зрение
- Решение систем линейных уравнений
- Машинное обучение и анализ данных
- Практические советы по использованию матриц
- Начинаем с простой системы уравнений
- Используйте программные инструменты
- Вопрос и ответ: Почему важно знать теорию матриц для современного специалиста?
Как применить теорию матриц в реальной жизни: практические советы и примеры
На первый взгляд теория матриц кажется сложной и абстрактной областью математики, которая предназначена лишь для специалистов и ученых. Однако, если взглянуть глубже, становится очевидным, что матрицы — это мощный инструмент, который широко используют во множестве практических сфер нашей жизни. От решения систем уравнений и обработки изображений до оптимизации процессов и анализа данных — теория матриц открывает перед нами безграничные возможности. В этой статье мы расскажем не только о фундаментальных принципах, но и о том, как применить теорию матриц в конкретных ситуациях, делая нашу жизнь проще и эффективнее. Вдохновляйтесь нашими практическими примерами и рекомендациями, чтобы понять, почему матрицы — это не только академическая тема, но и реально полезный инструмент.
Что такое матрица и как она представлена?
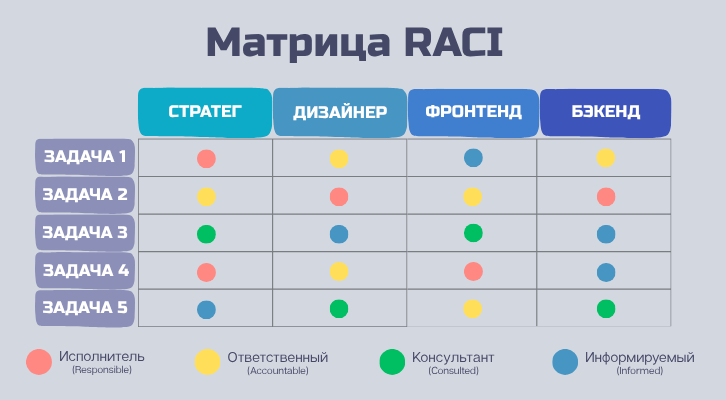
Для начала важно понять, что такое матрица. Простыми словами, матрица — это таблица чисел, организованных по строкам и столбцам. Обычно её используют для представления данных или преобразований, происходящих с ними. Такая таблица может выглядеть так:
| Александр | Марина | Игорь |
|---|---|---|
| 85 | 90 | 78 |
| 88 | 76 | 85 |
Матрицы могут быть разнообразных размеров:
- 2×2 (две строки и два столбца),
- 3×3 или больше,
- и даже более сложные, с большим количеством строк и столбцов.
Если говорить проще, то каждая точка в таблице — это элемент матрицы. Важно помнить, что операции с матрицами, такие как умножение, сложение или транспонирование, позволяют решать сложные задачи быстро и эффективно.
Применение теории матриц в различных сферах жизни
Обработка изображений и компьютерное зрение
Одним из наиболее заметных применений матриц является обработка изображений. Каждая фотография — это набор пикселей, каждый из которых представлен числовым значением яркости или цвета. Эти данные организованы в виде матриц, что позволяет:
- увеличивать или уменьшать изображение,
- применять фильтры для устранения шума,
- проводить распознавание объектов и даже создавать эффект художественной обработки.
Например, при использовании свертки (конволюции) — операции, основанной на матричных вычислениях — компьютерные программы «учатся» выявлять границы объектов, распознавать лица и даже анализировать медицинские снимки.
Решение систем линейных уравнений
Очень часто в практике сталкиваемся с задачами типа: найти неизвестные переменные, удовлетворяющие нескольким уравнениям одновременно. Для этого используют матрицы и методы их решения, такие как метод Гаусса или использование обратной матрицы.
- Пример: определить, сколько товаров нужно закупить по двум поставкам, чтобы обеспечить минимальные издержки при выполнении всех условий.
- Опыт показывает, что: грамотное использование матриц значительно ускоряет процесс и делает решения более точными.
| Условие | Решение |
|---|---|
| Множество уравнений по ассортименту и объему | Использование матриц и методов обращения для поиска оптимальных решений |
Машинное обучение и анализ данных
В современном мире теория матриц лежит в основе алгоритмов машинного обучения и искусственного интеллекта. Множество моделей, таких как нейронные сети и алгоритмы классификации, использует матрицы для представления входных данных, весовых коэффициентов и результатов работы сети.
- Обучение нейросетей — это последовательное обновление матриц весовых коэффициентов, чтобы минимизировать ошибку.
- Анализ больших данных — это обработка огромных объемов информации, представленной в виде матриц, чтобы выявить закономерности и сделать предсказания.
Пример:
Что такое матрица признаков в модели машинного обучения и зачем она нужна?
Ответ: Матрица признаков, это таблица данных, где каждый столбец представляет определенный признак (характеристику), а каждая строка — отдельный образец или объект. Она служит входом для алгоритмов обучения, позволяя системе находить закономерности и делать предсказания.
Практические советы по использованию матриц
Начинаем с простой системы уравнений
Для тех, кто только знакомится с матрицами, рекомендуем начать с решения простых систем уравнений. Для этого хорошо подойдет метод Гаусса или формула для обратной матрицы.
Например, рассмотрим систему:
2x + y = 5
x ⏤ y = 1
Эту систему можно представить в виде матриц и решить за пару минут, применяя стандартные алгоритмы.
Используйте программные инструменты
Сегодня существует множество программ и библиотек, которые облегчают работу с матрицами. Среди них — MATLAB, NumPy (Python), Octave, и даже Excel. Они позволяют:
- вводить, редактировать и визуализировать матрицы,
- выполнять автоматические операции,
- решать сложные системы и моделировать процессы.
Пример использования NumPy для решения системы уравнений:
import numpy as np
A = np.array([[2, 1], [1, -1]])
b = np.array([5, 1])
x = np.linalg.solve(A, b)
print(x)
Вопрос и ответ: Почему важно знать теорию матриц для современного специалиста?
В чем заключается ключевая ценность знания теории матриц для специалиста, работающего в сфере IT, маркетинга или инженерии?
Ответ заключается в том, что теории матриц лежит в основе множества современных технологий и методов анализа данных. Специалисты, которые умеют эффективно пользоваться матрицами, могут не только ускорить рабочие процессы, но и повысить точность своих решений. В области IT — это программирование, разработка алгоритмов и работы с большими данными. В маркетинге и экономике — это анализ рынка, прогнозирование и моделирование сценариев. В инженерных сферах — расчет систем, проектирование и автоматизация. Без знания основ матриц сегодня трудно представить себе современного профессионала, способного решать комплексные задачи и оставаться конкурентоспособным на рынке.
Подробнее — 10 популярных LSI-запросов к статье
| Матрицы для обработки изображений | Методы решения систем уравнений на основе матриц | Применение матриц в машинном обучении | Обработка данных с помощью матриц | Обучение нейросетей и матрицы |
| Интерпретация матриц в экономике | Теория матриц для инженеров | Почему важны матрицы в автоматике | Примеры использования матриц в программировании | Матрицы и системы анализа данных |
| Обратные матрицы и их применение | Линейная алгебра и матрицы | Модели машинного обучения и матрицы | Практическое применение матриц | Матричные вычисления в бизнесе |