- Погружение в мир квантовых корреляций: Математика за пределами классики
- Что такое квантовые корреляции?
- Математическая основа квантовых корреляций
- Измерение квантовых корреляций
- Научные приложения квантовых корреляций
- Квантовые вычисления и корреляции
- Квантовые сети и связь
- Философские аспекты квантовых корреляций
Погружение в мир квантовых корреляций: Математика за пределами классики
В нашем исследовательском путешествии мы предлагаем вам погрузиться в захватывающий мир квантовых корреляций, где привычные законы классической физики выходят за рамки и открывают новые горизонты. Мы обсудим, как математика и физика переплетаются в этой уникальной области, и как они помогают нам понять суть квантовых явлений.
Как наука о законах природы, квантовая механика ставит перед нами множество вопросов. Что такое корреляция в квантовом мире? Как она может быть физически интерпретирована и измерена? Ответы на эти вопросы и лежат в основе нашей статьи, что даст нам возможность понять фундаментальные аспекты информации и взаимодействия частиц на квантовом уровне.
Что такое квантовые корреляции?
Квантовые корреляции представляют собой уникальные связи между частицами, которые могут существовать, даже когда они находятся на значительном расстоянии друг от друга. Эти корреляции нарушают принципы локальности, с которыми мы привыкли иметь дело в классической физике. Главная идея заключается в том, что состояние одной частицы может моментально влиять на состояние другой, независимо от расстояния между ними.
Представьте себе два спина, которые созданы в паре. Если мы измерим спин одной частицы и получим значение «вверх», то спин другой частицы в тот же момент окажется «вниз», даже если они находятся на противоположных концах вселенной. Это явление, известное как «квантовая запутанность», стало основным объектом изучения в квантовой механике и в квантовой информации.
Математическая основа квантовых корреляций
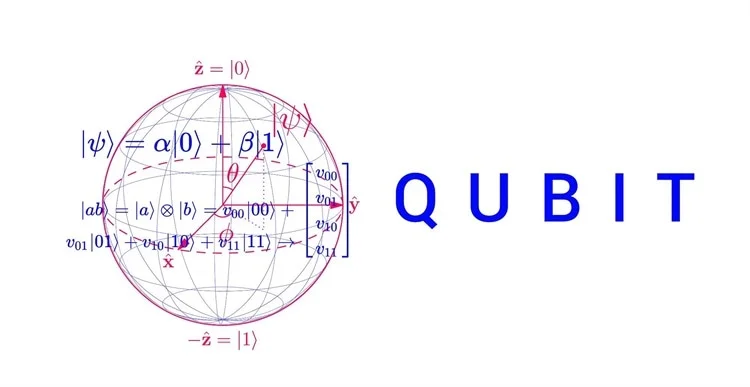
Чтобы понять, как работают квантовые корреляции, мы должны обратиться к математическому формализму. Основным инструментом здесь является векторное пространство, в котором каждое состояние системы описывается вектором состояния (или кетов). Важную роль в этом процессе играют операторы, которые действуют на состояния и могут изменить их.
Вектор состояния, расположенный в Гильбертовом пространстве, часто записывается в виде:
|ψ⟩ = α|0⟩ + β|1⟩,
где α и β – амплитуды вероятности для двух базисных состояний |0⟩ и |1⟩. Однако иногда нам необходимо рассмотреть системы, состоящие из нескольких частиц, что требует более сложного подхода и использования тензорного произведения.
При наличии двух частиц можно записать общее состояние как:
|Ψ⟩ = Σ_ij c_ij |i⟩|j⟩,
где c_ij представляют собой комплексные коэффициенты, которые описывают корреляции между состояниями. Эти матрицы коэффициентов дают нам возможность предсказать результаты измерений, основанные на принципах вероятности.
Измерение квантовых корреляций
Измерение квантовых корреляций часто осуществляется с помощью различных экспериментов, таких как тестирование неравенств Белла. Эти неравенства позволяют нам проверить наличие квантовых корреляций в системах, а также отличить их от классических корреляций. Суть неравенств Белла заключается в том, что если корреляции превышают определенный предел, то они должны иметь квантовую природу.
Эксперименты, подтверждающие квантовую корреляцию, часто используют сложные установки, где измерения выполняются независимо друг от друга. Это позволяет избежать влияния локальных скрытых переменных, которые могут определять результаты измерений в классической интерпретации.
Научные приложения квантовых корреляций
Квантовые корреляции имеют множество приложений в современной науке и технологии. Они играют ключевую роль в области квантовых вычислений и квантовой криптографии, где безопасность передаваемых данных достигается за счет использования принципов квантовой механики.
Например, в квантовой криптографии для шифрования информации используется явление, известное как «квантовое распределение ключей» (QKD). Здесь ключами служат физические состояния частиц, которые создаются в запутанном состоянии. Запутанность обеспечивает, что попытка перехвата или изменения ключа будет немедленно обнаружена.
Квантовые вычисления и корреляции
Квантовые вычисления используют принципы квантовых корреляций для обработки информации на совершенно новом уровне. Устройства, известные как квантовые компьютеры, способны решать задачи, которые являются непосильными для классических компьютеров благодаря параллельному проведению вычислений и быстрому взаимодействию между кубитами.
В квантовых вычислениях корреляции между кубитами обеспечивают более высокую скорость обработки данных и возможность решения задач, таких как факторизация больших чисел, которая может занять неимоверно большое количество времени на классических системах.
Квантовые сети и связь
Разработка квантовых сетей является еще одной многообещающей областью, где квантовые корреляции играют центральную роль. Такие сети могут быть использованы для передачи информации с помощью запутанных частиц, обеспечивая защиту от перехвата и несанкционированного доступа.
Реальные примеры квантовых сетей включают квантовую интернет-сеть, которую разрабатывают исследователи по всему миру. Она в первую очередь нацелена на создание безопасной связи между компьютерами и устройствами, используя квантовые принципы.
Философские аспекты квантовых корреляций
Квантовые корреляции поднимают множество философских вопросов, касающихся природы реальности и теории познания. Они оспаривают классические представления о causality (причинности) и детерминизме, ставя под сомнение, как мы понимаем взаимосвязь между объектами в нашей вселенной.
Множество ученых и философов обсуждали парадоксы, возникающие при попытках интерпретировать квантовые корреляции. Например, знаменитый парадокс Эйнштейна-Подольского-Розена (EPR) и обсуждаемые альтернативные интерпретации, такие как «многомировая интерпретация», подчеркивают сложность понимания фундаментальных аспектов квантового мира;
Мы завершили наш обзор математики квантовых корреляций и их значимости в современном мире науки и технологий. Понимание этих принципов открывает новые горизонты в области квантовых вычислений, криптографии и многочисленных приложений, которые они могут обеспечить.
В ближайшие годы ожидается дальнейшее развитие технологий, основанных на квантовых корреляциях. Исследования в этой области только начинают набирать обороты и, вероятно, приведут к новым открытиям и приложениям, которые мы пока даже не можем себе представить.
Каковы основные применения квантовых корреляций в современной науке и технике?
Основные применения квантовых корреляций включают квантовые вычисления, квантовую криптографию и создание квантовых сетей. Эти технологии используют принципы квантовой механики для обеспечения безопасности в коммуникациях и повышения вычислительных мощностей для решения сложных задач, которые недоступны классическим системам.
Подробнее
| Квантовая запутанность | Квантовые вычисления | Квантовая криптография | Неравенства Белла | Квантовые сети |
| Квантовые эффекты | Запутанные состояния | Философия квантовой механики | Квантовые технологии | Современные исследования |