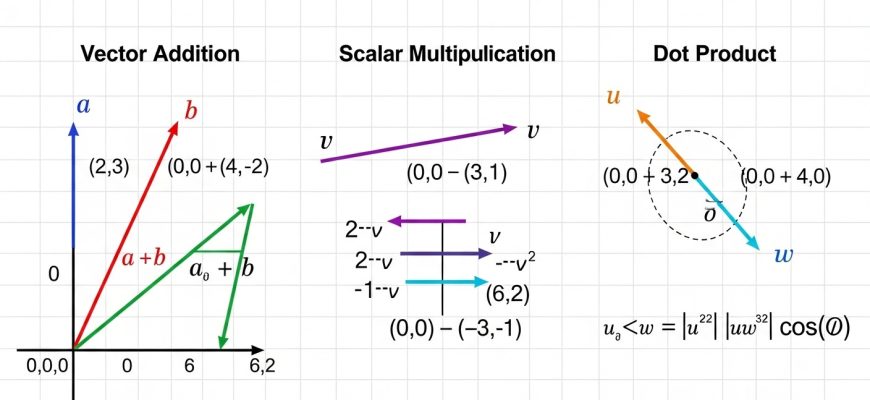
Погружение в мир линейной алгебры: операторы и наблюдаемые величины, раскрываем секреты важнейших концепций

Линейная алгебра — это фундамент современного математического мышления, без которого невозможно представить развитие таких областей, как физика, компьютерные науки, инженерия и статистика. В этой статье мы постараемся не только объяснить основные понятия, связанные с операторами и наблюдаемыми величинами, но и сделать так, чтобы материал стал максимально понятным, интересным и практическим. Вместе мы разберем, что именно скрывается за этими терминами, какие задачи они помогают решать, и как применять их в различных сферах деятельности.

Что такое операторы в линейной алгебре?

В простых словах, оператор, это особая функция, которая действует на векторы или матрицы, превращая их в новые объекты, сохраняя при этом свойства линейной комбинации. Представьте себе, что оператор, это некий "машина", которой можно подать вектор, и она вернет вам другой вектор, возможно, немного измененный, но при этом с сохранением определенных структурных характеристик.

Наиболее распространенными операторами в линейной алгебре являются:

Линейные операторы: преобразуют векторное пространство в себя или в другое векторное пространство, сохраняя операцию сложения и умножения на число.
Матрицы преобразования: конкрет управления действиями операторов в виде таблиц, которые позволяют удобно вычислять образ вектора.

Ключевые свойства операторов

Линейные операторы обладают рядом свойств, которые обеспечивают их удобство и универсальность:

Линейность: применение оператора к суммы двух векторов равно сумме результатов применения этого же оператора к каждому вектору отдельно.
Гомогенность: при умножении вектора на число оператор "масштабирует" результат на то же число.
Собственные векторы и собственные значения: важные понятия для анализа операторов, позволяющие находить особенности преобразований.

Что такое наблюдаемые величины в контексте линейной алгебры?

Наблюдаемые величины — это конкретные параметры или показатели, которые можно измерить или вычислить при работе с системами, моделями или данными. В линейной алгебре мы можем представлять наблюдаемые величины как результаты применения определенных операторов к векторным состояниям системы или модели.

Например, в механике наблюдаемыми величинами могут быть положение и скорость тела, а в статистике — среднее значение или дисперсия. В рамках математических моделей эти величины задаются через линейные комбинации элементов вектора состояния системы.

Значение наблюдаемых величин

Примеры	Описание	Использование
Положение	Результат наблюдения координат тела	Контроль траектории
Температура	Измерение температуры в системе	Моделирование процессов
Электрический ток	Измерение силы тока в цепи	Диагностика и управление

Связь между операторами и наблюдаемыми величинами

Это один из наиболее важных аспектов линейной алгебры, который помогает понять, как меняется один параметр в результате действия оператора. В частности, применение оператора к вектору состояния системы зачастую моделирует изменение системы или процессы ее развития, а наблюдаемые величины — это те параметры, которые мы получаем в результате этого преобразования и можем измерять или анализировать.

Рассмотрим аккуратный пример: есть оператор, моделирующий перемещение объекта. Тогда его наблюдаемые величины — это координаты и скорость. Анализ собственных векторов этого оператора покажет, в направлениях каких перемещается объект, а собственные значения, насколько сильны эти перемещения.

Практическое применение этой связи

Диагностика систем и элементов с помощью анализа собственных значений операторов.
Оптимизация процессов на основе изучения наблюдаемых параметров.
Моделирование поведения сложных систем — например, в экономике или биологии.

Глубже погружаясь: собственные векторы и собственные значения

Это один из ключевых инструментов, который помогает анализировать операторы. Собственные векторы, это такие векторы, которые при применении к ним оператора только масштабируются, а собственные значения — это коэффициенты масштабирования. Такой анализ позволяет понять фундаментальные свойства оператора и предсказать его поведение при многократных применениях.

Собственные значения и векторы используются для диагонализации операторов, что значительно упрощает вычисления и позволяет выделить важнейшие аспекты преобразований.

Практические этапы поиска собственных векторов и значений

Записать характеристический многочлен: det(A ⎯ λI) = 0, где A — матрица оператора, λ — собственное значение, I, единичная матрица.
Найти корни этого многочлена — это собственные значения.
Для каждого λ решить систему уравнений (A ⎯ λI)v = 0, получить собственный вектор;

Понимание операторов и наблюдаемых величин в рамках линейной алгебры открывает широкие возможности для анализа систем, моделирования их поведения и оптимизации процессов. Это не только теоретическая база, но и практический инструмент для инженеров, ученых, аналитиков и просто любознательных, стремящихся понять закономерности окружающего мира.

Изучая эти концепции, мы учимся видеть глубинные связи между различными параметрами, что помогает принимать более обоснованные решения и создавать инновационные решения в различных сферах.

Вопрос: Почему важно изучать операторы и наблюдаемые величины в рамках линейной алгебры?

Изучение операторов и наблюдаемых величин важно потому, что они позволяют моделировать реальные системы, анализировать их поведение, предсказывать последствия изменений и оптимизировать процессы. Эти концепции лежат в основе современных методов обработки данных, системного анализа и различной инженерной практики, что делает их незаменимым инструментом для научных исследований и технологического развития.

Подробнее

Линейные операторы	Собственные векторы	Наблюдаемые параметры систем	Модели на основе линейных операторов	Анализ систем по наблюдаемым величинам
Аналитические методы в линейной алгебре	Диагонализация операторов	Применение собственных значений	Модели в физике и инженерии	Обработка данных и машинное обучение
Ролевые модели систем	Связь операторов и системных характеристик	Примеры наблюдаемых величин	Обоснование важности анализа	Практическое применение анализа
Фундаментальные понятия линейной алгебры	Методы поиска собственных величин	Преобразование систем через операторы	Инженерные решения и исследования	Статистические и аналитические подходы

Погружение в мир линейной алгебры операторы и наблюдаемые величины раскрываем секреты важнейших концепций