- Погружение в мир матриц: как применять теорию матриц для решения практических задач
- Что такое матрицы и зачем они нужны?
- Основные операции с матрицами
- Практическое использование теории матриц
- Пример 1: Решение систем линейных уравнений
- Пример 2: Анализ экономических процессов
- Расширенные возможности: матрицы и алгоритмы машинного обучения
- Например, анализ изображений и обработка сигналов
Погружение в мир матриц: как применять теорию матриц для решения практических задач
Когда мы слышим слово «матрица», на ум зачастую приходят матрицы в математике, а также всевозможные схемы и таблицы в повседневной жизни. Однако, за этим словом скрывается гораздо больше, чем кажется на первый взгляд. Теория матриц — это мощный инструмент, который применяется в самых разных областях, начиная от инженерии и науки до экономики и компьютерных технологий. В нашей статье мы расскажем о том, как именно использовать принципы работы с матрицами для решения реальных практических задач, и поделимся собственным опытом, который поможет вам понять все тонкости и возможности.
Что такое матрицы и зачем они нужны?
Перед тем, как перейти к конкретным примерам применения, важно понять, что собой представляет матрица. Это двумерный массив чисел, расположенных в строках и столбцах. По сути, матрица — это таблица, которая служит для систематизации информации и упрощения вычислений.
В реальной жизни матрицы помогают моделировать ситуации, где необходимо учитывать множество факторов одновременно. Какие бы области ни рассматривать, физику, экономику или программирование — матрицы оказываються универсальным инструментом для упорядочивания и анализа данных.
Основные операции с матрицами
- Сложение и вычитание: Позволяют комбинировать данные или находить разницу между различными наборами информации.
- Умножение: используется для моделирования преобразований, например, вращений или масштабирований.
- Обратные матрицы: позволяют решать системы линейных уравнений.
- Транспонирование: меняет местами строки и столбцы, что важно для аналитики и преобразований.
Практическое использование теории матриц
Теперь перейдем к самому важному — как применять теорию матриц в реальных задачах. Ответ лежит в области моделирования, оптимизации и анализа данных. Наш опыт показывает, что правильное понимание и использование матриц значительно ускоряет решение сложных задач, повышая точность и эффективность;
Пример 1: Решение систем линейных уравнений
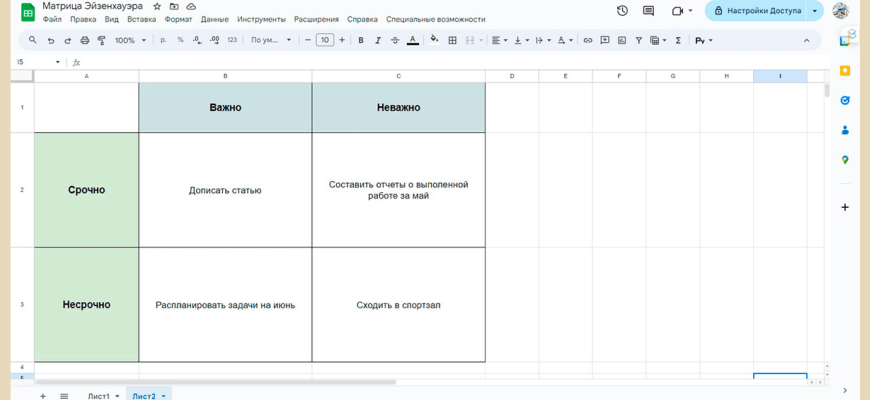
Одним из наиболее частых применений матриц является решение систем уравнений. Например, представим, что мы анализируем ресурсы на предприятии и хотим понять, как распределить временные стандарты по различным отделам.
| Отдел | Время (часов) | Ресурсы |
|---|---|---|
| Производство | 40 | Материалы |
| Логистика | 25 | Транспорт |
| Маркетинг | 15 | Рекламные кампании |
Используя матрицы коэффициентов ресурсов и времени, мы можем лучше понять, как перераспределить нагрузку или оптимизировать работу — все через умножение и решение систем уравнений, выраженных через матрицы.
Пример 2: Анализ экономических процессов
В экономике существует область, называемая Input-Output моделированием, где матрицы используются для анализа взаимосвязей между отраслями. Представим таблицу, в которой указано, сколько продукции каждой отрасли поставляется другим.
| Отрасль-источник | Отрасль-получатель | Объем (единиц) |
|---|---|---|
| Электроника | Автоматизация | 1000 |
| Машиностроение | Строительство | 300 |
| Электроника | Энергетика | 500 |
Анализируя такие таблицы и создавая матрицы взаимозависимостей, мы можем спрогнозировать развитие промышленности, оптимизировать производство или даже выявлять узкие места в логистике.
Расширенные возможности: матрицы и алгоритмы машинного обучения
Сегодня невозможно игнорировать связь между теорией матриц и современными технологиями. В частности, машинное обучение и искусственный интеллект основаны на операциях с матрицами. Их использование позволяет находить паттерны, обучать нейросети и делать предсказания на основе больших данных.
Попадая в сферу разработки алгоритмов, мы сталкиваемся с задачами оптимизации, кластеризации и распознавания изображений, в которых матрицы — это ядро операционных процессов.
Например, анализ изображений и обработка сигналов
В обработке изображений каждое изображение представлено матрицей пикселей, а преобразования — разными матричными операциями. Мы можем редактировать, фильтровать и улучшать изображения, а также обучать системы распознавать объекты.
На практике, умение применять теорию матриц — это ключ к быстрому и точному решению задач. В нашем опыте с разными задачами мы убедились, что правильный подбор методов и инструментов помогает достигать целей гораздо эффективнее. Начинайте экспериментировать, моделировать и находить новые подходы — и результат не заставит себя ждать.
Вопрос: Почему изучение теории матриц так важно для современного специалиста и как оно помогает в решении практических задач?
Ответ: Потому что матрицы — это универсальный язык, который помогает моделировать, анализировать и оптимизировать любые системы, где есть взаимодействия между множеством элементов. Понимание операции с матрицами позволяет быстрее находить решения сложных систем уравнений, оптимизировать процессы, создавать интелектуальные системы и анализировать большие объемы данных.
Подробнее
| как применять матрицы в экономике | пример использования матриц в машинном обучении | решение систем уравнений матрицами | оптимизация процессов через матрицы | использование матриц в графическом анализе |
| матрицы для моделирования физических процессов | обработка изображений матрицами | алгоритмы матриц для нейросетей | примеры оптимизации с помощью матриц | аналитика и визуализация данных |
| межотраслевой анализ и макроэкономика | использование матриц в робототехнике | преобразование данных через матрицы | разработка программных решений | создание графических моделей |
| вычисление матриц в физике и инженерии | матричные методы в статистике | методы оптимизации с матрицами | аналитические инструменты | новые тренды в использовании матриц |
| системы управления и автоматизация | лабораторные исследования | алгоритмы обработки данных | современные методики анализа | инновационные решения |