Погружение в тайны физики элементарных частиц: теория представлений
Добро пожаловать в увлекательный мир фундаментальных частиц и их загадок! В этой статье мы попробуем разобраться в сложной, но очень важной области современной физики — теории представлений․ Это один из ключевых методов описания поведения элементарных частиц, который помогает понять, почему частицы ведут себя именно так, а не иначе, и как строится современная модель Вселенной на самом фундаментальном уровне․
В течение наших исследований и наблюдений ученые пришли к выводу, что все окружающее нас разнообразие, это всего лишь различные проявления нескольких фундаментальных объектов — элементарных частиц․ Однако чтобы понять, как эти частицы взаимодействуют и что определяет их свойства, понадобилось углубиться в теорию, основанную на математических структурах, а именно — на теориях групп и их представлениях․
В этой статье мы подробно расскажем о том, что такое теория представлений, как она применяется к физике элементарных частиц, и почему она считается одним из наиболее важных инструментов в физике․ Погрузимся в историю её развития, разберем основные понятия, а также посмотрим на современные примеры и их роль в научных открытиях․
Что такое теория представлений? Основные понятия
Теория представлений — это раздел математики, изучающий способы отображения абстрактных групп в пространственных структурах, таких как пространства векторов․ В контексте физики элементарных частиц это помогает описывать свойства частиц при сохранении симметрий систем․
Когда мы говорим о symmetries — или симметриях в физике — мы имеем в виду свойства системы, которые остаются неизменными при определенных преобразованиях․ Например, вращение системы вокруг своей оси или изменение ее положения в пространстве могут не влиять на ее основные характеристики․
Наиболее важное влияние на развитие теории представлений оказали работы Эндрю Вилса, Виллема Исти и многих других ученых, которые показали, как можно связать свойства групп, таких как группа вращений SO(3) или группа Лоренца — с характеристиками частиц․
Основные термины:
- Группа, математическая структура, которая описывает множество элементов и операции их объединения, оставляющей структуру системы неизменной․
- Представление группы, конкретное отображение элементов группы в линейные операции на векторных пространствах․
- Модуль — пространство, на которое действует группа, и в материальной физике ассоциируется с состояниями частиц или полями․
Таким образом, теория представлений позволяет нам реализовать абстрактные симметрии в понятные и пригодные для физических расчетов формы․ Именно благодаря этому подходу мы можем понять, почему у частицы есть определённые свойства, как она взаимодействует с другими частицами, и как остается сохраняться при различных преобразованиях․
Роль теории представлений в физике элементарных частиц
Физика элементарных частиц — это область, где симметрии и их представления занимают центральное место․ Самые фундаментальные частицы, такие как кварки, лептоны и фотон, описываются с помощью специальных представлений групп, например, группы Лоренца и внутренней симметрии, связанной с "цветом" кварков и спином․
Несколько ключевых групп, используемых в физике, включают:
- Группа Лоренца, описывает преобразования в пространстве-времени, связанные с движением со скоростью света и относительно других систем отсчета․
- Угловая группа SO(3) — отвечает за вращательные симметрии в пространстве․
- Группа унитарных преобразований U(1), SU(2), SU(3) — связаны с внутренними симметриями, определяющими взаимодействия и свойства частиц․
Используя представления указанных групп, физики смогли классифицировать все общие характеристики частиц и понять механизм взаимодействий․ Например, спин-статистика, заряд, цвет и другие свойства выражаются через определенные представления групп․ Так, понятие "спин" у частиц — это конкретное представление группы вращений, а электромагнитное взаимодействие связано с группой U(1)․
Ключевые достижения в применении теории представлений:
- Классификация элементарных частиц по их спинам и внутренним симметриям․
- Обоснование существования кварков через представления SU(3), отвечающей за цветовое взаимодействие․
- Разработка теории электрослабого взаимодействия, где групповые структуры обеспечивают механизм массового получения частиц․
Без этих математических подходов описания и предсказания новых элементов физической модели было бы невозможным;
История развития и современные направления
История теории представлений восходит к началу XX века, когда математики и физики начали тесно сотрудничать для поиска универсальных языков описания симметрий․ Наиболее яркими этапами стали работы Эйнштейна, Гамильтона, Лиувилля и других, разрабатывавших основы групповой теории и ее применения в физике․
В середине века развитие теории групп и ее представлений привело к созданию Стандартной модели — теории, которая объединяет электромагнитное, слабое и сильное взаимодействия․ В ее основе лежит идея, что все взаимодействия отличаются только разными представлениями унитарных групп․
Современные направления исследования включают:
- Обобщение теории представлений для поиска новых частиц и сил․
- Изучение спинорных представлений, связанных со спинами фермионов и бозонов․
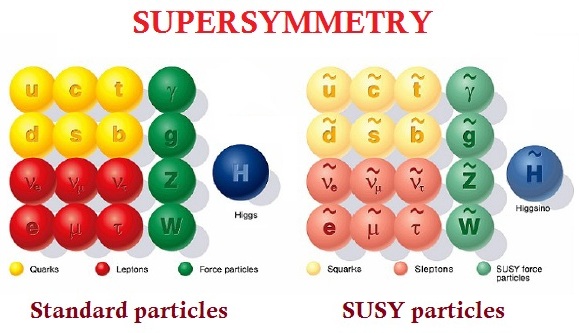
- Разработка теорий за пределами Стандартной модели — теория суперсимметрии, теория струн и другие․
Эти направления помогают ученым искать ответы на вопросы о природе темной материи, гравитации на квантовом уровне и возможности объединения всех взаимодействий в единую теорию․
Мы можем с уверенностью сказать, что теория представлений — это один из краеугольных камней современной физики․ Без понимания симметрий, групп и их отображений было бы невозможно построить модели, объясняющие свойства и взаимодействия элементарных частиц․ Эти знания позволяют не только описывать текущий мир, но и делать предсказания о свойствах новых, еще не открытых частиц и полей․
Разбирая сложные структуры системы через представления групп, мы делаем шаг к глубокому пониманию устройства Материи и Вселенной в целом․ Остается надеяться, что дальнейшее развитие этой области станет ключом к разгадке самых великих тайн природы — от происхождения мира до природы самой материи․
Как использовать теорию представлений для понимания свойств новых частиц, которые еще не открыты?
Использование теории представлений в поиске новых частиц заключается в анализе предполагаемых симметрий и соответствующих им групп․ Теоретики моделируют возможные представления этих групп, предсказывают, какие свойства могут иметь новые частицы, и разрабатывают экспериментальные методы их обнаружения на ускорителях․ Таким образом, теория становится не только инструментом для объяснения уже известных фактов, но и мощным средством предсказания новых открытий․
Подробнее
| теории групп | симметрии в физике | классификация частиц | представления групп | фундаментальная физика |
| группы Лоренца | применение групп в физике | кварки и лептоны | модели элементарных частиц | прогнозы в физике |