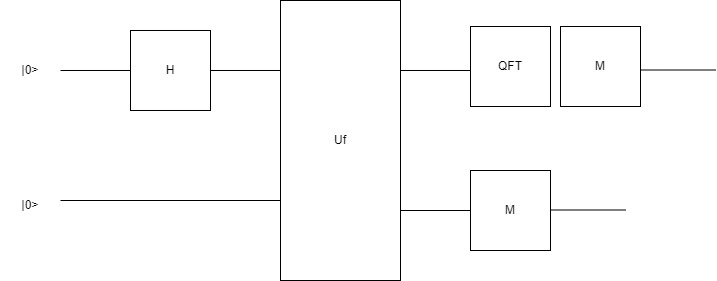
- Погружение в тайны квантовых ошибок: как работают коды Шора и зачем они нужны
- Что такое квантовые ошибки и почему их нужно исправлять?
- Основы теории квантовых кодов исправления ошибок
- Ключевые понятия квантовых кодов
- Код Шора: изобретение, открывающее новые горизонты
- История появления и основные идеи
- Принцип работы кодов Шора
- Ключевые особенности и преимущества
- Практическое применение и вызовы
- Вопрос к статье
Погружение в тайны квантовых ошибок: как работают коды Шора и зачем они нужны
Квантовая технология обещает революцию в вычислительной индустрии, системах безопасности и симуляции сложных процессов. Однако, как и в классической электронике и информатике, квантовые системы сталкиваются с фундаментальной проблемой — ошибками. Именно поэтому развитие теории устранения ошибок в квантовых вычислениях является одним из самых важных и захватывающих направлений современной науки. В ходе нашей статьи мы подробно разберем одну из самых известных и фундаментальных техник — коды Шора, которые позволяют исправлять квантовые ошибки и делать квантовые компьютеры более надежными. Погружаясь в эту тему, мы постараемся сделать сложные концепции понятными для каждого читателя, независимо от его уровня подготовки.
Что такое квантовые ошибки и почему их нужно исправлять?
Если мы говорим о работе квантовых компьютеров, то сразу возникает вопрос — а как обеспечить правильность их работы? В классической вычислительной технике это делается с помощью проверки контрольных сумм, резервных копий и других методов. В квантовых систем все гораздо сложнее, потому что сама природа квантовых состояний очень хрупкая, и даже небольшая внешняя возмущенность способна разрушить информацию.
Квантовые биты, или кубиты, обладают уникальной характеристикой — способностью находиться в суперпозиции нескольких состояний одновременно. Это делает вычисления невероятно мощными, но одновременно уязвимыми. Малейшее взаимодействие с внешней средой, шум, магнитные поля либо тепловое воздействие могут привести к возникновению ошибок, которые разрушают запутанные состояния и выводят систему из строя.
Обнаружить и исправить эти ошибки крайне важно, иначе квантовые алгоритмы потеряют смысл. Обеспечивая устойчивость системы, мы дополняем возможность квантовых вычислений реально применимыми сценариями — например, в криптографии, моделировании молекул или оптимизации.
| Типы квантовых ошибок | Описание |
|---|---|
| Деградация фазы | Несовпадение фазовых состояний кубитов, ведущее к искажению суперпозиции. |
| Амплитудные ошибки | Изменение амплитуд состояний, что может привести к неправильному результату. |
| Деконнект и потеря информации | Потеря связей между кубитами, разрывы в запутанности. |
Проблема заключается в том, что исправление ошибок в классическом смысле невозможно реализовать полностью в квантовой системе без нарушения квантовой суперпозиции. Поэтому нужны особые методы — именно они и были разработаны в виде квантовых кодов исправления ошибок.
Основы теории квантовых кодов исправления ошибок
Классические коды исправления ошибок основаны на простых и понятных концепциях: дублирование информации, контрольные суммы, кодирование в более крупные блоки. В квантовой же механике ситуация усложняется из-за принципа несуперпозиции, запрета клонирования состояний и необходимости соблюдать квантовую механику; Именно поэтому появились специальные квантовые коды, среди которых особое место занимает код Шора.
Классический код, например, использует тройку битов для защиты одного бита: если один бит ошибся, по двум остальным можно восстановить исходное значение. В квантовой системе ситуация сложнее: необходимо одновременно исправлять ошибки амплитуд и фаз, не разрушая при этом состояние кубита.
Общая идея — это внедрение концепции из классических кодов, адаптированная под требования квантовой механики, а именно — возможность исправлять ошибки без клонирования и измерения состояния напрямую.
Ключевые понятия квантовых кодов
- Кодирование в кодовые пространства: создание специальных подпространств, которые позволяют обнаружить и исправить ошибки.
- Обнаружение ошибок: с помощью измерений, которые не нарушают квантовую информацию, устанавливается факт возникновения ошибки.
- Исправление ошибок: восстановление исходного состояния без разрушения его квантовых свойств.
Различные типы ошибок требовали разных решений, и одна из наиважнейших задач — разработка универсальных методов, способных работать со многими случаями ошибок.
Код Шора: изобретение, открывающее новые горизонты
Самое известное достижение в области квантовых кодов — это создание алгебраической техники, известных как коды Шора. Эти коды были предложены выдающимся ученым Питером Шором в 1995 году и с тех пор считаются одними из самых мощных инструментов для исправления ошибок в квантовых вычислениях.
Коды Шора позволяют обнаружить и исправлять как амплитудные, так и фазовые ошибки, обеспечивая тем самым высокая надежность квантовых систем. Что делает их особенно важными, способность исправлять ошибки, которые мощные квантовые алгоритмы могут порождать при выполнении сложных операций.
История появления и основные идеи
- Появление: Теория была сформирована в середине 1990-х годов в ответ на необходимость повышения надежности квантовых вычислений.
- Идея: построение специальных квантовых кодов, которые используют свойства запутанности для обнаружения и исправления ошибок.
- Реализация: включает сложные операции, которые «кодируют» логическую информацию в более крупные системы кубитов.
Принцип работы кодов Шора
Коды Шора используют многоступенчатое кодирование, в рамках которого логическая информация (бит) распределяется между множеством физических кубитов. Основные шаги включают:
- Кодирование исходных данных: преобразование логического кубита в состояние, распределенное по нескольким физическим кубитам.
- Обнаружение ошибок: с помощью специальных измерений, которые не нарушают суперпозицию, выявляются признаки ошибок.
- Исправление ошибок: при наличии ошибок происходит их устранение без разрушения информации.
"Ключ к эффективности кодов Шора — использование свойства дефектастической запутанности и возможности коррекции ошибок без разрушения квантового состояния."
Ключевые особенности и преимущества
- Коррекция ошибок на уровне квантовых битов: позволяют сохранить целостность и точность вычислений.
- Мощь при работе с шумами: подходят для квантовых систем с высоким уровнем ошибок.
- Обеспечение масштабируемости: позволяют расширять квантовые сети без потери надежности.
Практическое применение и вызовы
Несмотря на свои преимущества, коды Шора требуют очень большого количества физических кубитов для защиты даже небольшой логической единицы информации. Это создает определенные технические сложности — реализовать достаточно эффективные и масштабируемые кодовые системы сегодня еще сложно. Однако прогресс не стоит на месте, и уже сегодня идет активная работа по внедрению подобных методов в области квантовых устройств и экспериментов.
Ключевые области применения:
| Область | Описание |
|---|---|
| Квантовые вычислительные платформы | Обеспечение надежности разработанных алгоритмов и систем. |
| Безопасность информации | Квантовая криптография и защита данных. |
| Образовательные проекты | Обучение новым методам от теории до практики. |
Вместе с тем, существует множество вызовов — потребность в более эффективных алгоритмах кодирования, сокращение количества кубитов, совершенствование технологий измерения и исправления ошибок.
"Без последующих её улучшений, реализация практических квантовых компьютеров останется отдаленной мечтой."
Развитие теории квантовых ошибок и создание эффективных кодов исправления — это основа для развития квантовых технологий в целом. Коды Шора остаются мощным инструментом, открывающим новые горизонты в области надежных квантовых вычислений. И хотя на пути их практической реализации стоит много технических и теоретических вызовов, прогресс уже идет.
Обучаясь и совершенствуя эти методы, ученые и инженеры создают фундамент для будущих квантовых систем, способных выполнять сложные задачи, которые недоступны классическому компьютеру. В этой области нас ожидает множество удивительных открытий и технологических прорывов.
Вопрос к статье
Почему важно развивать и внедрять квантовые коды исправления ошибок, такие как коды Шора?
Ответ: Развитие квантовых кодов исправления ошибок, таких как коды Шора, критически важно для достижения стабильных и масштабируемых квантовых систем. Эти коды позволяют обнаруживать и исправлять ошибки, возникающие из-за слабых взаимодействий с окружающей средой, что обеспечивает надежность квантовых вычислений, широко расширяет их практически возможное применение и способствует развитию квантовой криптографии, моделирования и новых технологий в целом. Без таких методов квантовые компьютеры останутся недоступными для практического использования из-за высокой чувствительности к ошибкам.
Подробнее
| коды исправления ошибок в квантовых систем | принципы работы квантовых кодов | технологии реализации кодов Шора | проблемы масштабирования квантовых ошибок | преимущества квантовых кодов |
| квантовые алгоритмы исправления ошибок | примеры использования кодов Шора | технологические вызовы в квантовых кодах | будущее квантовых ошибок | квантовая криптография и коды ошибок |