Применение теории мер в квантовой механике: как математика помогает понять загадки микромира

Когда мы задумываемся о том, как устроен наш мир на самом фундаментальном уровне, перед нами открываются невероятные сложности. Квантовая механика — одна из самых загадочных и одновременно важных теорий в современной физике. Она раскрывает странные свойства частиц, волновые свойства, вероятностную природу событий и множество других феноменов, которые кажутся непостижимыми на первый взгляд. Однако за всеми этими загадками стоит глубинная математическая структура — теория мер, которая помогает формализовать и понять происходящее на квантовом уровне.

В этой статье мы окунемся в мир теории мер и расскажем, как именно она применяется в квантовой механике. Постараемся сделать это максимально понятно и интересно — ведь наука должна вдохновлять, а не пугать. Нашей задачей является показать, что математика — это не просто сухая абстракция, а мощный инструмент, раскрывающий тайны микромира и делая их доступными для осмысления.

Что такое теория мер и почему она важна в квантовой механике?

Для начала важно понять, что представляет собой теория мер. Это раздел математической аналитики, в которой изучаются размеры, вероятности и распределения. Простыми словами, теория мер помогает ответить на вопрос: как "распределены" различные объекты или события в пространстве?

В классической физике мы привыкли к понятиям плотности и вероятности, которые присущи статистической механике и теории вероятностей. В квантовой механике же эти идеи обретают особую важность. Именно наличие строгой математической основы — теории мер — позволяет формализовать такие понятия, как вероятность обнаружения частицы в определенной области пространства и связи между состояниями.

Косвенное применение теории мер: квантовые состояния и вероятность

Одним из ключевых аспектов использования теории мер является описание квантовых состояний. В классической механике состояние системы — это точка в фазовом пространстве, и распределения вероятностей задаются функциями плотности. В квантовой же механике всё гораздо абстрактнее: состояние системы задается вектором в гильбертовом пространстве, а физические величины — это операторы в этом пространстве.

Однако, чтобы связать эти абстракции с наблюдаемыми величинами, вводится понятие спектра оператора и мера спектральных разложений, которое базируется на теории мер. Это позволяет нам определить вероятность обнаружения частицы в определенной области пространства или со значением определенной энергии. Теория мер, в данном случае, служит мостом между математической формализацией и физической интерпретацией.

Меры в спектральной теории: как она помогает описать квантовые системы

В квантовой механике важной концепцией является спектральная разложение операторов. Каждый оператор, связанный с наблюдаемой, имеет спектр — множество возможных значений, которые может принимать физическая величина.

Спектральная теория, основанная на теории мер, позволяет разложить оператор по его спектру с помощью специальной меры — так называемой спектральной меры. Это значительно упрощает вычисление вероятностей и помогает понять, как именно распределены возможные результаты измерений в феноменах, сталкивающихся в микроокружении.

Наименование	Описание	Применение в квантовой механике	Пример
Спектральная мера	Мера, присвоенная оператору, которая позволяет разложить его по спектру	Определение вероятностей измерения конкретных значений	Вероятность обнаружения энергетического уровня
Рассширение мер	Обобщение мер, позволяющее работать со сложными случайными величинами	Работа с операторными функциями и неограниченными операторами	Расчёт вероятностей для операторов, не имеющих ограниченного спектра

Меры в квантовой динамике: описание эволюции состояния

Кроме статического описания, важной задачей является понимание того, как состояние системы меняется со временем. В классической механике это описывается уравнением Хойнинга или уравнением Лямпорта — дифференциальными уравнениями для плотности вероятностей.

В квантовой механике, благодаря теории мер, вводится понятие квантовой динамики через меры, которые отражают новые состояния системы. Это особенно важно при рассмотрении диффузионных процессов и квантовых потоков. Теория мер позволяет формалировать такие процессы максимально точно и аналитически.

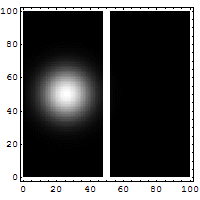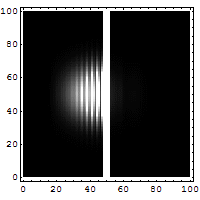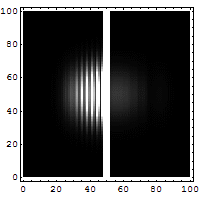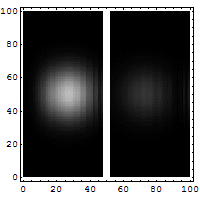
Пример: динамика частицы в потенциальной яме

Рассмотрим пример частиц, движущейся в потенциальной яме. Ее состояние задается вектором в гильбертовом пространстве, и его эволюция описывается уравнением Шредингера. Используя спектральную теорию и меры спектра, можно построить функцию распределения вероятностей для находки частицы в конкретной области в любой момент времени. Это помогает понять, как волновая функция "расползается" и проявляет характерные интерференционные явления, связанные с вероятностной природой микромира.

Подробнее

Теория мер в квантовой механике	Спектральная мера	Динамика частицы	Значение теории мер	Квантовые операторы
Спектр оператора	Вероятности и распределения	Квантовая динамика	Временная эволюция	Квантовые эффекты