Применение теории вероятностей в квантовой метрологии: как точность измерений меняет наш мир

В современном мире точность измерений играет решающую роль во множестве областей — от разработки новых материалов до систем связи и навигации․ Особенно важными становятся границы возможностей измерения, которые позволяют нам достигать предельных значений в технологических процессах․ Именно здесь на сцену выходит квантовая метрология — новая граница точности и изобретательности, где теория вероятностей занимает ключевую роль․ Мы вместе попробуем понять, как же именно теоретические основы вероятностных процессов помогают создавать сверхчувствительные приборы, и как это влияет на развитие науки и технологий․

Что такое квантовая метрология и зачем она нужна

Квантовая метрология — сравнительно молодая область науки, которая занимается разработкой и применением квантовых технологий для измерения физических величин с непревзойденной точностью․ В отличие от классической метрологии, где используют макроскопические приборы, основанные на классических законах физики, квантовая метрология использует свойства квантовых систем — такие как когерентность, запутанность и суперпозиция․ Эти свойства позволяют создать измерительные приборы, которые превосходят по точности свои классические аналоги, достигая границ, определённых законами квантовой механики․

На практике это означает создание атомных часов с точностью, превышающей миллионы раз точность обычных механических или электронных часов, или сенсоры для обнаружения минимальных изменений в гравитационных полях․ Такие достижения находят применение в гидрографии, геодезии, а также в тестировании фундаментальных законов физики․ Важнейшую роль здесь играет теория вероятностей, которая помогает понять и управлять неопределенностями, присущими квантовым системам․

Почему теория вероятностей — основа квантовой измерительной техники

Суть квантовых измерений коренится в понимании того, что квантовые системы не имеют строго определённых значений физических величин до момента измерения․ Вместо этого, эти значения описываются вероятностными распределениями, заданными волновыми функциями или плотностями вероятности․

Использование теории вероятностей в этом контексте позволяет нам моделировать и предсказывать поведение квантовых систем, учитывать неопределённости и ошибочные отклонения, а также оптимизировать процедуры измерений․ В квантовой метрологии это проявляется в создании интерферометров, которые используют вероятностные интерференционные эффекты для повышения чувствительности․ Таким образом, теория вероятностей становится инструментом для определения максимально возможной точности измерения и минимизации погрешностей․

Основные принципы и методы применения вероятностных моделей в квантовой метрологии

Понимание того, как использовать теорию вероятностей в квантовой механике, осуществляется через ряд специальных методов и принципов, таких как:

• Оценка параметров: для определения истинных значений физических параметров на основе набора данных используют методы оценки, такие как байесовская и оценка максимальной правдоподобности․
• Кривая Фишера и пределы точности: фишеровская информация помогает оценить граница возможной точности измерений
• Квантовое дробление ошибок: использование запутанных состояний для уменьшения неопределённости в измерениях
• Квантовые операторы и плотностные матрицы: модели, позволяющие описывать вероятностные состояния системы и предсказывать их эволюцию

Все эти принципы базируются на вероятностных моделях, что позволяет нам достигать максимально возможных результатов в условиях квантовых ограничений․

Примеры использования теории вероятностей в практике квантовой метрологии

Рассмотрим несколько реальных сценариев, где теория вероятностей помогает повысить точность измерений․

Имплементация интерферометров с запутанными фотонами

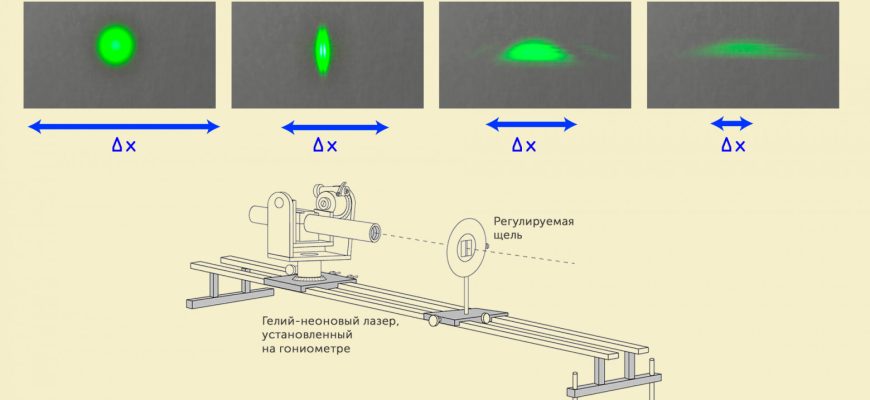
Интерферометры — это приборы, основанные на эффекте интерференции света․ Использование квантовых запутанных фотонов позволяет повысить чувствительность этих устройств․ Вероятностные модели помогают определить, как подготовить систему для минимизации ошибок и оптимизации результатов․

Параметр	Классическое значение	Квантовое значение
Чувствительность	до 1/√N (где N — число фотонов)	до 1/N

Оценка качества кварцевых часов

Использование вероятностных методов позволяет более точно определить границы погрешности и повысить стабильность системы, что критически важно для навигационных систем GPS и других технологий

Преимущества использования вероятностей в квантовой метрологии

Главное достоинство этого подхода, возможность работы в условиях неопределённости и погрешностей, характерных для квантовых систем․ Мы можем:

1. Создавать измерительные приборы с предельно высокой чувствительностью
2. Разрабатывать методы оценки погрешностей и ошибок
3. Использовать запутанные состояния для достижения границ теоретической точности
4. Обеспечивать надежную и точную работу систем в сложных условиях

Современные тренды и перспективы развития

В будущем развитие квантовой метрологии во многом будет основываться на совершенствовании моделирования вероятностных процессов․ Новые алгоритмы и методы, основанные на машинном обучении, позволяют автоматизировать обработку данных и повысить точность измерений․ Важным направлением является создание гибридных систем, использующих классические и квантовые элементы, а также расширение границ измеряемых величин․

Понимание теории вероятностей — это неотъемлемая часть современного научного мышления и практики․ В квантовой метрологии эта теория становится главным инструментом для достижения новых высот точности, что открывает перед человечеством невероятные возможности в исследованиях, технологиях и прикладных задачах․ Освоение этих методов, залог успеха в построении будущего, где границы измерения будут смещены далеко за пределы нынешних возможностей․

Подробнее

Квантовая интерференция и вероятности	Запутанность в метрологии	Квантовые оценки параметров	Пределы измерения в квантовой механике	Использование плотностных матриц
Примеры квантовых сенсоров	Моделирование ошибок в квантовой метрологии	Обучение машинному вкладу в метрологию	Роль байесовских методов	Будущее квантовых измерений