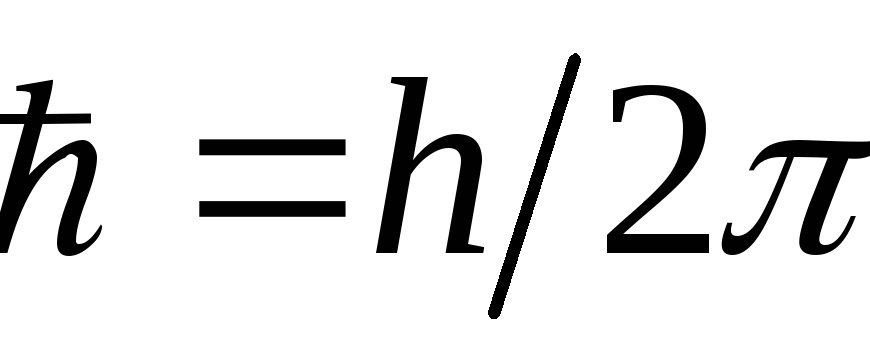Специальные функции в решении уравнения Шрёдингера: Герми́т и Лежа́ндр
Когда мы углубляемся в мир квантовой механики и, в частности, в уравнение Шрёдингера, мы сталкиваемся с множеством интересных концепций, одна из которых — это специальными функциями. В рамках наших исследований мы обнаружили, что функции Герми́та и Лежа́ндра играют ключевую роль в этой области. Эти функции представляют собой решение для различных физических систем и препятствий, и мы уверены, что их изучение станет полезным не только студентам, но и более опытным физикам. Давайте подробнее разберемся в их свойствах, методах применения и связи с уравнением Шрёдингера.
Уравнение Шрёдингера — это одно из основополагающих уравнений квантовой механики, описывающее, как состояние квантовой системы изменяется во времени. Оно играет аналогичную роль в квантовой механике, как уравнение Ньютона в классической физике. Уравнение принимает форму:
iħ ∂ψ/∂t = Hψ
где ψ — это волновая функция системы, H — оператор Гамильтона, а ħ — редуцированная постоянная Планка. Решение этого уравнения для различных потенциальных полей и условий ведет нас к использованию специальных функций, таких как функции Герми́та и Лежа́ндра.
Роль специальных функций
Специальные функции — это функции, которые возникают в решениях различных дифференциальных уравнений и имеют важные аналитические свойства. В контексте уравнения Шрёдингера, эти функции предоставляют необходимые математические инструменты для нахождения решений в специфических условиях, таких как в потенциале ящика или в атомной модели.
- Система с простым гармоническим осциллятором (функции Герми́та)
- Проблема о сферически симметричном потенциале (функции Лежа́ндра)
- Возможности аппроксимационных методов и вариационного принципа
Специальные функции Герми́та
Функции Герми́та являются решениями дифференциального уравнения, известного как уравнение Герми́та. Эти функции часто возникают в контексте простого гармонического осциллятора. Обозначение для функции Герми́та — Hn(x), где n — это порядковый номер функции, а x — переменная. Они выражаются следующим образом:
| n | Hn(x) |
|---|---|
| 0 | 1 |
| 1 | 2x |
| 2 | 4x2 ⎯ 2 |
| 3 | 8x3 ‒ 12x |
Эти функции обладают важными свойствами, такими как ортогональность. Это особенно полезно в квантовой механике, где позволяет изолировать решения для различных квантовых чисел.
Применение функций Герми́та
Решение уравнения Шрёдингера с использованием функций Герми́та применяется, прежде всего, в системах, описывающих колебательные движения, такие как молекулы и атомы. Мы можем наблюдать это в конкретном примере: простом гармоническом осцилляторе.
Запись волновой функции может быть выражена как:
ψn(x) = An Hn(x) e-x²/2
где An — нормировочная константа. В этом контексте функции Герми́та служат основой для построения всех возможных состояний системы.
Специальные функции Лежа́ндра
Функции Лежа́ндра возникают в контексте решения математических задач, связанных с сферической симметрией. Они являются решениями уравнения Лежа́ндра, которое имеет множество применений в физике, включая электро- и магнито-статические поля.
Обозначение для функции Лежа́ндра будет Pn(x), где n — это порядковый номер функции. Эти функции могут быть определены через интегральные представления и имеют следующие свойства:
| n | Pn(x) |
|---|---|
| 0 | 1 |
| 1 | x |
| 2 | (3x2 ⎯ 1)/2 |
| 3 | (5x3 ⎯ 3x)/2 |
Применение функций Лежа́ндра
В контексте уравнения Шрёдингера функции Лежа́ндра помогают нам находить решения для потенциалов, имеющих сферическую симметрию, таких как потенциальные ямы и атомные орбитали. Здесь волновая функция может быть выражена в следующем виде:
ψlm(r, θ, φ) = Rl(r) Ylm(θ, φ)
где Ylm — сферическая функция на основе функций Лежа́ндра, а Rl — радиальная часть волновой функции.
Связь между функциями Герми́та и Лежа́ндра
Несмотря на то, что функции Герми́та и Лежа́ндра применяются в разных контекстах, их связь тонка и интересна. Оба типа функций имеют ортогональные свойства и могут быть использованы для построения решений уравнения Шрёдингера для различных потенциальных полей.
Можно сказать, что эти функции представляют два разных подхода к решению одной и той же проблемы — описанию поведения квантовых систем под действием различных сил и излучений. Основные идеи и методы, стоящие за этими функциями, помогают глубже понять структуру и динамику квантовых систем.
Изучая специальные функции в контексте уравнения Шрёдингера, мы понимаем их критическую роль в квантовой механике и физике в целом. Функции Герми́та и Лежа́ндра не только предоставляют мощные математические инструменты, но и открывают двери к пониманию более сложных теорий и моделей. При помощи этих функций мы можем исследовать не только простые системы, такие как гармонические осцилляторы, но и сложные структуры, такие как атомы и молекулы, что, безусловно, добавляет глубину в наше понимание атомной мира.
Как специальные функции Герми́та и Лежа́ндра влияют на наши понимания квантовой механики и физики в целом?
Мы считаем, что специальные функции Герми́та и Лежа́ндра играют ключевую роль в теоретической физике; Они не только упрощают множество сложных расчетов, но и придают структуру нашим знаниям о микромире. Используя их, мы можем анализировать новые квантовые системы и находить более точные предсказания их поведения.
Подробнее
| Квантовая механика | Уравнение Шрёдингера | Специальные функции | Функции Герми́та | Функции Лежа́ндра |
| Гармонический осциллятор | Сферическая симметрия | Квантовая система | Ортогональные функции | Физические модели |