Теория представлений групп Ли: погружение в глубокую структуру симметрий

Когда мы сталкиваемся с концепцией симметрии в природе и математике, зачастую у нас возникает ощущение что это что-то очень абстрактное и далекое от реальности․ Однако, как только мы начинаем углубляться в теорию групп Ли и их представления, открывается завеса магии, которая позволяет понять внутреннюю структуру объектов, стоящих за самыми элементарными и сложными системами․ Именно эта теория лежит в основе многих современных областей физики, математики и даже инженерных наук․ Сегодня мы расскажем о том, что такое теория представлений групп Ли, почему она так важна и как она помогает раскрывать тайны сложных систем․

Что такое группы Ли и почему они важны?

Группы Ли — это объединение понятий группы и гладкой (непрерывной) структуры, которая задает правила перемещения и симметрии в пространстве․ Их название связано с именем норвежского математика Sophus Lie, который впервые начал исследовать непрерывные группы в конце XIX века․ Вот основные моменты, которые помогут лучше понять, что это такое:

Группы — это множества элементов, такие как движения, преобразования или операции, объединенные по определенным правилам, например, обратимость и ассоциативность․
Ли-группы — это группы, у которых структура задается гладкой дифференцируемой многообразной структурой, позволяющей применять методы анализа․
Примеры групп Ли: вращения в пространстве, трансляции, линейные преобразования․

Эти группы описывают все возможные симметрии физических систем, что делает их основой для теорий о строении Вселенной, микро- и макрообъектах․

Значение теории представлений групп Ли

Теперь, когда мы поняли основные идеи о группах Ли, важен аспект — их представления․ Теория представлений позволяет нам отображать абстрактные группы как группы линейных преобразований векторных пространств, что существенно упрощает их изучение и применение․

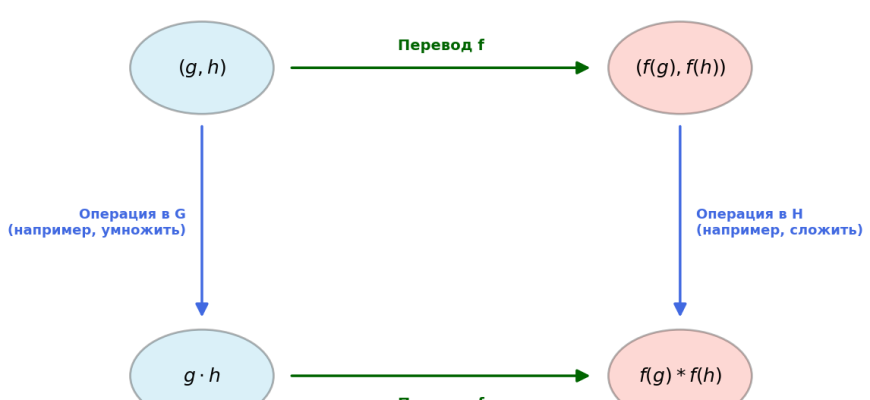
Представление группы — это гомоморфизм из группы в группу линейных обратимых преобразований, что позволяет "расписать" сложные симметрии в виде матриц․
Зачем нужны представления? Они позволяют анализировать абстрактные симметрии через более понятные и наглядные инструменты линейной алгебры․
Практическое применение: квантовая механика, теория поля, кристаллография, робототехника, что подтверждает важность этой теории․

Основные понятия и строение теории представлений групп Ли

Рассмотрим более подробно, как строится теория представлений групп Ли и какие ключевые элементы в этом процессе встречаются․

Лингвистика основных концепций

В основе теории лежат следующие важные термины:

Модули иекторные пространства: в них реализуются линейные представления групп․
Нейтральное и непрерывное представление: определяет, как объекты меняются под действием элементов группы․
Классы эквивалентостей: помогают различать и классифицировать все возможные представления․

Классические примеры и их использование

Рассмотрим основные типы представлений:

Тип	Описание	Пример
Фундаментальные представления	Наиболее простое и важное, где группы реализуются через действия на базовых векторных пространствах	Вращения в 3D, SO(3)
Изолированные представления	Операции, которые остаются внутри определенного подпространства	Сопряженные преобразования
Реальные и комплексные представления	В зависимости от типа поля, на котором действует группа	Реальные — физические системы, комплексные — квантовая механика

Ключевые теоремы и методы исследования представлений

На практике для изучения представлений групп Ли используют множество мощных теорий и инструментов․ Одним из них является разложение по единичным компонентам, которое позволяет разлагать сложные задачи на более простые․ Также важнейшие теоремы включают:

Теорема о полной классификации неподвижных представлений
Теорема о разложении по конечномерным представлениям
Иерархия неподвижных и регулярных представлений

Эти методы позволяют ученым и инженерам применять теорию в самых различных сферах, начиная от физических моделей до разработки алгоритмов машинного обучения, основанных на симметриях․

Практическое применение теории представлений групп Ли

Давайте рассмотрим, где же именно проявляется эта теория в реальной жизни и как она помогает решать сложные задачи:

Физика: теория поля, квантовая механика, теория струн — все основываются на понимании симметрий и их представлений․
Кристаллография: описание структур и свойств материалов через симметрии кристаллических решеток․
Инженерное дело: робототехника, динамика систем, разработка навигационных алгоритмов․
Компьютерные науки: машинное обучение и алгоритмы, основанные на анализе симметрий и групповых структур․

Область применения	Конкретные задачи	Результат
Физика	Анализ симметрий физических систем, квантовые состояния	Упрощение уравнений, предсказания новых эффектов
Машинное обучение	Анализ данных через симметрии и групповые методы	Более эффективные алгоритмы и модели
Химия и материалы	Классификация структур, предсказание свойств	Разработка новых материалов и веществ

Погружаясь в глубины теории групп Ли и их представлений, мы понимаем, насколько фундаментальными являются эти концепции для развития науки и технологий․ Постоянное расширение границ наших знаний, способность моделировать сложные системы и находить новые связи в структуре материи — все это достигается именно благодаря этим мощным инструментам․ Они помогают не только лучше понять окружающий мир, но и создавать новые технологии, формы искусства и даже новые способы взаимодействия с информацией․ Поэтому исследования в области групп Ли и их представлений остаются актуальными и востребованными сегодня и в будущем․

Как объяснить сложную и абстрактную математическую теорию простым языком? Ответ, через её применение в реальной жизни․ Теория групп Ли, один из ярких примеров того, как глубокие идеи находят воплощение в тех областях, где кажется невозможным — от квантовой физики до современных гаджетов․

Подробнее

1	группы Ли для начинающих	классификация представлений групп Ли	математика и физика особенности групп Ли	примеры групп Ли	группы Ли в квантовой механике
2	модельные представления групп Ли	группы симметрий и их роль	стеханография групп Ли	представления групп в физике	применение групп Ли в химии

Теория представлений групп Ли погружение в глубокую структуру симметрий