Теория представлений: как она раскрывает тайны элементарных частиц

Когда мы задумываемся о строении вселенной на самом фундаментальном уровне, перед нами возникает множество загадок и вопросов․ Что такое элементарные частицы? Как они взаимодействуют друг с другом? Какие теории позволяют нам понять их природу и поведение? В этой статье мы подробно рассмотрим одну из ключевых концепций современной физики, теорию представлений․ Эта теория служит мощным инструментом для описания элементарных частиц и их взаимодействий, позволяя понять их посредством математических структур и симметрий․

На протяжении всей истории физики ученым удавалось открыть всё новые уровни реальности, благодаря применению абстрактных математических методов․ Теория представлений, на наш взгляд, является одной из таких методов, которая соединяет воедино экспериментальные данные и теоретические модели․ Вместе мы разберемся, что же это за теория, какие у неё есть важные аспекты и как она помогает раскрывать тайнописание микромира․

Что такое теория представлений и почему она так важна?

Чтобы понять значение теории представлений, начнем с определения․ В широком смысле, теория представлений, это математическая структура, которая описывает, каким образом задаются и преобразуются элементы симметрий в рамках физических систем․ В физике элементарных частиц она помогает классифицировать частицы по их внутренним свойствам, таким как спин, заряд и другие квантовые числа, а также предсказывать их поведение при взаимодействиях․

Один из важных аспектов заключается в том, что все элементарные частицы, несмотря на свою видимую разнообразность, могут быть объединены и классифицированы в рамках групповых структур․ Эти группы — это симметрии, неизменные при определенных преобразованиях․ Теория представлений занимается тем, что связует эти группы с конкретными типами физических объектов, описывая их «представления»․ Такой подход облегчает анализ и предсказания новых феноменов в микромире․

Преимущество теории представлений	Обеспечивает универсальный и систематический подход к классификации частиц и их взаимодействий․
Применение	Используется при разработке моделей стандартной теории, расширениях и новоменьших теориях․
Ключевой инструмент	Математическая структура групп и их представлений, которая связывает симметрии и свойства частиц․

Исторический контекст и развитие идеи

История теории представлений начинается ещё в XX веке, когда ученые столкнулись с необходимостью систематизировать огромное разнообразие экспериментальных данных о частицах и их взаимодействиях․ В 1920–1930-х годах возникло понимание, что симметрии играют ключевую роль в физике, что привело к формализации идеи групп и их представлений как инструмента для описания квантовых систем․

Особенно значительным этапом стало развитие групповой теории в рамках квантовой механики и теории поля․ В 1950-х годах появились первые классификации частиц по их свойствам с помощью представлений групп Ли, таких как SU(2) и SU(3)․ Это стало основой для построения Стандартной модели, которая на сегодня является наиболее успешной теорией микромира․

Основные понятия и математические инструменты

Чтобы понять, как работает теория представлений, необходимо познакомиться с рядом ключевых понятий и инструментов․ В первую очередь, это группы и их представления, где группы отражают симметрии физических систем, а представления — конкретные способы их реализации в виде математических объектов․

Группы и их свойства

• Группа, множество элементов, объединенных операцией, которая задает преобразования симметрий․
• Линейное представление — способ отображения элементов группы в матрицы, действующие на векторные пространства․
• Левые и правые преобразования — означают свойства симметрии и её реализации в пространстве состояний․

Представления групп

1. Образец входных данных: у группы есть множество представлений — различных способов реализовать ее действия․
2. Явление инвариантности: физические свойства не изменяются при действии элементов группы․
3. Роль в классификации: каждое представление соответствует типу частицы, характеризуемой её квантовыми числами․

Эти инструменты позволяют переводить абстрактные симметрии в конкретные математические объекты, что в свою очередь дает возможность делать предсказания о свойствах элементарных частиц․

Роль групп и симметрий в физике частиц

Наиболее важным аспектом применения теории представлений является понимание того, как групповые симметрии влияют на физические свойства частиц․ Например, чтобы описать спин, используют представления группы SU(2), которая связана с вращательными симметриями․ Для описания кварков, цветовых зарядів и сильных взаимодействий применяется группа SU(3)․

Кроме того, роль симметрий появляется в сохранении физических величин — например, законы сохранения энергии, импульса, заряда, а также более сложных квантовых чисел․ Когда существующие симметрии расширяются или нарушаются, это ведет к новым изучаемым эффектам, что делает теорию представлений непререкаемым инструментом в исследованиях элементарных частиц․

Практическое применение и технологии

Современные акселераторы и эксперименты позволяют получать новые данные, которые помогают проверить теоретические предсказания․ Теория представлений позволяет моделировать результаты этих экспериментов, предсказывать новые частицы или феномены, что существенно ускоряет научный прогресс․

Например, предсказания о существовании бозона Хиггса были сделаны на основе теорий, построенных с использованием групповых структур, а его обнаружение — важное подтверждение правильности подхода․

Классификация частиц с помощью представлений

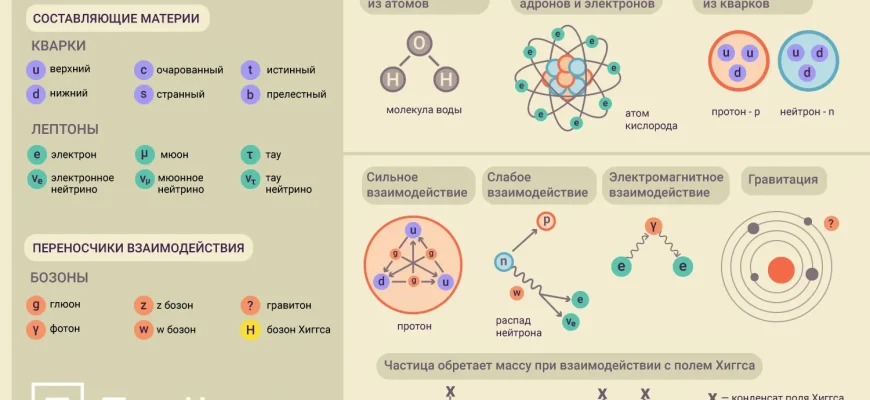
• Кварки, лептоны и бозоны — все они классифицированы по их представлениям в рамках групп SU(3), SU(2) и U(1)․
• Разобраться в взаимодействиях помогает анализ представлений, соответствующих различным квантовым числам․
• Понимание этих взаимодействий лежит в основе современных теорий и экспериментов․

Будущее теории представлений и открытия

Несмотря на впечатляющие успехи, теория представлений продолжает развиваться․ Новые модели, такие как теория суперсимметрий, теория струн и гравитационные расширения, используют более сложные группы и представления для описания неизвестных пока аспектов Вселенной․ В перспективе ожидается, что эти теории помогут решить такие важные загадки, как природа темной материи, происхождение космического инфляционного расширения и объединение всех фундаментальных взаимодействий․

Обещает дальнейшее расширение наших знаний и развитие технологий, которые позволяют экспериментально проверять гипотезы, основанные на теориях представлений․

Изучая и применяя теорию представлений, мы получаем мощный инструмент для классификации, анализа и предсказания свойств элементарных частиц․ Эта теория служит связующим звеном между абстрактной математикой и реальными экспериментами, помогая раскрывать тайны микромира и строить более полное понимание устройства вселенной․ От классических моделей до современных расширений — всё это свидетельствует о том, что симметрии и их представления, это язык, на котором говорит фундаментальная физика․

Итак, теория представлений — не просто сложная математика․ Это мощный инструмент, который помогает ученым не только систематизировать текущие знания, но и открывать новые горизонты в понимании сути микромира․ Мы уверены, что дальнейшие исследования в этой области принесут еще больше удивительных открытий, меняющих наше восприятие реальности․

Подробнее

групповая теория	симметрии в физике	классификация элементарных частиц	группы Ли	представления групп
квантовые числа	теория стандартной модели	модель кварков	групповая симметрия	представления SU(3)
группы и их свойства	примеры физической симметрии	динамика элементарных частиц	примеры групп в физике	специальное и общее теория ретикуляции
современные модели физики	акселераторы и опыт	предсказания теории	естественные симметрии	будущее теории групп
микробирузм и симметрии	группы в математике	построение модели Вселенной	инвариантность	скейлинговые симметрии