Теория вероятностей и правило Борна: как принимать правильные решения в условиях неопределенности

---

На протяжении всей истории человечества мы сталкиваемся с ситуациями, когда важно оценить вероятность события или принять решение на основе неполных или случайных данных. От выбора пути в дороге до анализа бизнес-рисков — все эти ситуации требуют понимания основных принципов теории вероятностей. Особенно ценными в этом контексте является правило Борна — мощный инструмент, который помогает корректно обновлять наши оценки и принимать обоснованные решения.

Что такое теория вероятностей и почему она важна?

---

Теория вероятностей — это раздел математики, изучающий случайные явления, их закономерности и методы количественной оценки неопределенности. Она помогает понять, насколько вероятно наступление того или иного события и как делать прогнозы при наличии ограниченной информации.

Например, при броске кубика вероятность получить число «6» равна 1/6 — это простейший случай, который показывает, как можно использовать фундаментальные понятия теории вероятностей в повседневной жизни. Однако в реальности ситуация зачастую усложнена, ведь данные могут быть неполными, а события — зависимыми или условными. Вот тут и вступает в силу правильное использование этих знаний.

Ключевые понятия теории вероятностей

---

Понятие	Описание	Пример
Вероятность события	числовая оценка того, насколько вероятно наступление события	Вероятность выпадения «орла» при броске монеты — 0,5
Условная вероятность	вероятность наступления события при условии, что другое событие уже произошло	Вероятность заболеть гриппом при наличии симптомов
Зависимые и независимые события	зависимые — события, исход одного влияет на другой; независимые — не влияют	Броски кубика — независимы; вытягивание карты и её возвращение — зависимы
Объединение и пересечение событий	объединение, событие, которое происходит при наступлении хотя бы одного из событий; пересечение, при наступлении обоих одновременно	Объединение: выпадение чисел ≥4 или равных 2 на кубике; пересечение: выпадение числа 3 и 4 одновременно невозможно

Что такое правило Борна и почему оно важно?

---

Правило Борна (или теорема Борна) — это фундаментальный результат в теории вероятностей, который помогает обновлять оценки вероятностей, исходя из дополнительной информации. Иными словами, это способ «пересчета» вероятности события с учетом наблюдений, очень важная концепция для принятия решений в условиях неопределенности.

Например, у нас есть две коробки с шариками: одна с 10 красными и 10 синими, а другая с 20 красными и 0 синими. Мы случайным образом выбираем коробку и извлекаем шарик. Если мы вытягивали красный шарик, как обновить вероятность, что мы взяли именно вторую коробку? Вот тут и помогает правило Борна, оно позволяет скорректировать первоначальные оценки на основе новых данных.

Пример использования правила Борна

---

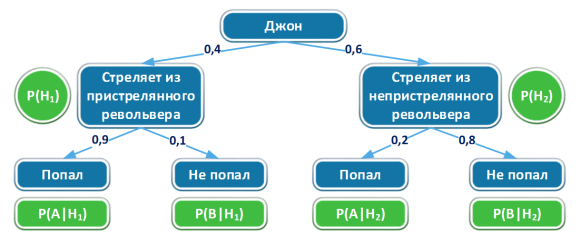
Рассмотрим наиболее типичный пример, диагностика болезни. Пусть у нас есть тест на заболевание, и его точность известна: вероятность положительного результата при наличии болезни (чувствительность) равна 0,9, а вероятность ложноположительного результата при отсутствии болезни (специфичность) — 0,8. Вероятность того, что человек заболеет, до теста равна 0,01;

Если тест показывает положительный результат, как повысить вероятность того, что человек действительно болен? Тут и используют правило Борна, которое помогает объединить исходные данные (априорную вероятность и качество теста) и получить апостериорную вероятность — вероятность болезни при положительном результате.

Формула правила Борна

P(Болезнь|Положительный тест) =  (P(Положительный тест|Болезнь) * P(Болезнь)) / P(Положительный тест)

Где:

• P(Болезнь|Положительный тест) — апостериорная вероятность болезни после положительного теста;
• P(Положительный тест|Болезнь) — чувствительность теста (0,9);
• P(Болезнь) — априорная вероятность заболевания (0,01);
• P(Положительный тест) — общая вероятность положительного теста, которая считается по формуле:

Вероятность	Расчет
P(Положительный тест)	= P(Положительный тест|Болезнь) * P(Болезнь) + P(Положительный тест|Нет болезни) * P(Нет болезни)
= 0,9 * 0,01 + (1 ‒ 0,8) * 0,99	= 0,009 + 0,198 = 0,207

Подставляем значения и рассчитываем:

P(Болезнь|Положительный тест) = (0,9 * 0,01) / 0,207 ≈ 0,009 / 0,207 ≈ 0,0435 или 4,35%

Это показывает, что несмотря на положительный тест, вероятность того, что человек действительно болен, невысока, всего около 4.35%. Такой пример демонстрирует важность правильных расчетов и понимания, как дополнительная информация влияет на окончательную оценку.

Практическое применение правила Борна

---

Применение правила Борна широко распространено в медицине, финансовых рынках, инженерных системах и даже в повседневных ситуациях. Вот несколько ключевых областей:

• Медицина: Обновление вероятности диагноза после получения новых данных.
• Бизнес-анализ: Оценка эффективности маркетинговых кампаний на основании поведения клиентов.
• Исследования и эксперименты: Корректировка гипотез при получении новых экспериментальных данных.
• Безопасность: Оценка угрозы или подозрительных действий на базе ранее известных сценариев.

---

Основная ценность теории вероятностей и правила Борна — это возможность систематически учитывать новую информацию и корректировать свои оценки. В современном мире, полном случайных факторов, умение правильно интерпретировать данные и пользоваться этими инструментами позволяет принимать более обдуманные и рациональные решения. Не стоит полагаться лишь на интуицию — проведите расчет, проанализируйте и основывайтесь на статистике.

Подробнее

Вероятность событий	Обучение теории вероятностей	Правило Борна для начинающих	Примеры из медицины и бизнеса	Обновление вероятностей
Условные вероятности	Зависимые и независимые события	Формулы и расчет	Применение в принятии решений	Общая информация и статьи