- Теория возмущений: мощный инструмент для анализа и моделирования сложных систем
- Что такое теория возмущений?
- Основные принципы метода
- Практическое применение теории возмущений
- Анализ колебаний и динамики
- Электротехника и электроника
- Квантовая механика и физика частиц
- Экономика и финансы
- Разбор математической основы метода
- Общее уравнение и его разложение
- Подставление и получение уравнений для членов ряда
- Преимущества и ограничения метода
- Практический пример: моделирование малых колебаний пружинной системы
Теория возмущений: мощный инструмент для анализа и моделирования сложных систем
Когда мы сталкиваемся с изучением сложных физических, инженерных или математических систем, зачастую возникает необходимость понять, как небольшие изменения или возмущения влияют на поведение всей системы в целом. Именно для такого анализа и была разработана теория возмущений, которая предлагает уникальные методы приближения решений уравнений и моделей, основанных на суммировании малых отклонений.
В этой статье мы подробно разберем, что такое теория возмущений, как она применяется в различных областях науки и техники, а также познакомимся с практическими примерами использования этого метода. Наше путешествие по миру возмущений поможет вам лучше понять фундаментальные принципы и научиться применять их для решения реальных задач.
Что такое теория возмущений?
Теория возмущений — это математическая техника, используемая для анализа систем, в которых параметры или условия немного отклоняются от известных, идеально решаемых случаев. В основном этот метод применяется для поиска приближенных решений дифференциальных уравнений или уравнений математической физики, когда точные решения найти сложно или невозможно.
Идея заключается в том, чтобы представить решение в виде суммы основного решения (без возмущений) и ряда дополнительных поправок, вызванных малым возмущением. Такой подход часто применяется в различных областях: механике, квантовой теории, гидродинамике, электротехнике, а также в экономике и биологии.
Основные принципы метода
- Выделение малого параметра. Вначале определяется небольшой параметр, характеризующий величину возмущения, например, малое число ε, которое служит мерой отклонения от исходной модели.
- Расширение решения в ряды. Решение системы ищется в виде разложение по степеням этого малого параметра: X = X₀ + εX₁ + ε²X₂ + ….
- Построение уравнений для каждого члена ряда. Подставляя разложение в исходное уравнение, получаем последовательные уравнения для каждого члена.
- Решение полученных уравнений и объединение. После нахождения отдельных компонент, получаем приближенное решение системы.
Практическое применение теории возмущений
Практическое использование метода позволяет значительно упростить решение сложных задач и раскрыть важные свойства систем, которые трудно или невозможно получить точным методом. Рассмотрим несколько примерных сфер применения:
Анализ колебаний и динамики
В механике и аэродинамике теория возмущений помогает моделировать небольшие отклонения от равновесных состояний, например, колебания мостов, самолетных крыльев или колебания маятника при малых амплитудах. Это позволяет обеспечить безопасность конструкции и понять ее поведение при различных воздействиях.
Электротехника и электроника
В области анализа цепей и систем электропитания, возможность учитывать небольшие искажения, паразитные сопротивления или нелинейные эффекты позволяет создавать более точные модели и разрабатывать надежные схемы.
Квантовая механика и физика частиц
В квантовой теории возмущения является фундаментальным методом для оценки поправок к энергиям, состояниям и другим квантовым свойствам систем. Например, при анализе взаимодействий, когда точные решения уравнений Шрёдингера недоступны, теория возмущений дает ценные приближения.
Экономика и финансы
В экономике модели с малыми возмущениями применяются для оценки воздействия незначительных изменений рынка или политики, что помогает инвесторам и аналитикам принимать более взвешенные решения.
Разбор математической основы метода
Понимание математической базы теории возмущений важно для того, чтобы правильно использовать этот инструмент. Ниже приведены основные этапы математического подхода.
Общее уравнение и его разложение
Пусть у нас есть дифференциальное уравнение вида:
L(X) = 0
где L — дифференциальный оператор, а X — искомое решение. В модели с возмущениями предполагается, что решение X можно представить в виде разложения:
| Обозначение | Значение |
|---|---|
| X | = X₀ + εX₁ + ε²X₂ + … |
| Где | — ε — малый параметр возмущения |
Подставление и получение уравнений для членов ряда
Подставляя разложение в исходное уравнение, получаем в виде суммы членов, равных нулю по степени ε. Тогда для каждого порядка получаются свои уравнения:
- Базовое уравнение: L(X₀) = 0
- Первого порядка: L'(X₀)X₁ + Q₁ = 0
- Второго порядка и выше: Аналогичным образом, формируются уравнения для X₂, X₃ и т.д..
Преимущества и ограничения метода
Метод возмущений чрезвычайно мощный и универсальный, однако имеет свои ограничения. Основные плюсы и минусы:
| Плюсы | Минусы |
|---|---|
|
|
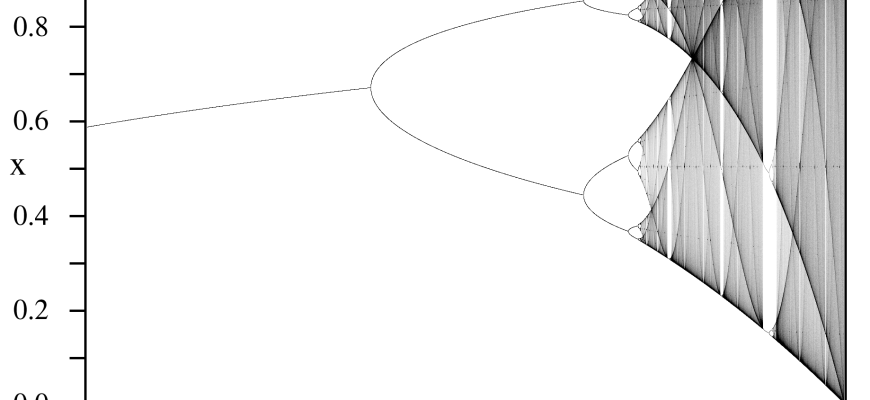
Практический пример: моделирование малых колебаний пружинной системы
Рассмотрим классический пример — систему масс, прикрепленную к пружине. В идеальной ситуации, когда пружина не оказывает сопротивления, а сила восстанавливает отклонение пропорционально смещению, решение определяется простым дифференциальным уравнением.
Теперь добавим небольшой нелинейный компонент, описываемый сопротивлением или малыми нелинейными силами. Используем теорию возмущений, чтобы найти приближенное решение этого устройства при малых отклонениях.
| Параметр | Описание |
|---|---|
| ε | Маленький параметр, характеризующий нелинейность |
| X | Общее смещение системы, разложенное в ряды |
| X₀ | Решение для линейной системы |
| X₁, X₂, … | Поправки, вызванные малыми нелинейными эффектами |
По мере решения уравнений на каждом этапе мы получим более точное описание поведения системы при малых возмущениях, что поможет инженерам и физикам более точно оценить надежность и характеристики конструкции.
Что бы ни сталкивались вы — со строительством, моделированием физических процессов или анализом экономических моделей — использование методов теории возмущений поможет находить разумные приближения и принимать обоснованные решения.
Вопрос: Почему теория возмущений считается таким важным инструментом в современной науке и технике?
Ответ: Потому что она позволяет получать приближенные решения сложных проблем, где точное решение недоступно, и лучше понять влияние небольших изменений на поведение системы, что особенно ценно при проектировании, анализе и оптимизации в различных областях науки и техники.
Подробнее
| Приближения в механике | Модель нелинейных систем | Анализ колебаний | Квантовые поправки | Финансовые модели |
| классические методы возмущений | теория слабых возмущений | приближения для дифференциальных уравнений | квантовые коррекции | финансовые риски |
| методы математического анализа | нелинейные системы | моделирование поведения | расчеты поправок | макроэкономика |
| теоретические основы | классическая механика | предсказание поведения систем | теории поля | инвестиционные стратегии |
| примеры и задачи | модели аэродинамики | анализ устойчивости | приближение энергии | риски в экономике |